I was invited to give a tutorial at the ANU-MSI Mini-course/workshop on the application of computational mathematics to plasma physics, and I thought it would be instructive to design a Particle-In-Cell (PIC) code from scratch and solve the simplest possible equation describing a plasma, namely the Vlasov-Poisson system in 1D. The idea was to illustrate:
- how simple, efficient and robust such numerical schemes are;
- how complex the non-linear phase-space dynamics and the onset of instabilities can be, e.g. bump on tail, two-stream, etc…
During the lecture, I invited people to download the pic-vlasov-plasma python sources from git, fire up their favourite editor and start filling in the blanks. At first, people were surprised by this nontraditional delivery, but were finally quite pleased to play an active role. Nothing is more effective than “learning by doing”.
The 1D collisionless Vlasov-Poisson model
consists of an advection equation for the probability distribution function ![]() of each species (ions and electrons in our case) subject to the mean electrostatic field produced by local charge imbalance, namely
of each species (ions and electrons in our case) subject to the mean electrostatic field produced by local charge imbalance, namely
![]()
where ![]() is the gradient of the electrostatic potential obtained by solving
is the gradient of the electrostatic potential obtained by solving
![]()
with charge densities ![]() given by the zeroth moment of the distribution function in velocity-space.
given by the zeroth moment of the distribution function in velocity-space.
As such, the Vlasov-Poisson system is a rather nasty integro-differential system of equations. The PIC method turns the Vlasov part into a system of ODEs by following a large number of tracers or macro-particles in phase-space (method of characteristics). The distribution function is approximated by a sum of point-charges ![]() . The PIC method turns the Poisson part into a matrix equation by depositing the charge carried by those macro-particles on a mesh, and subsequently inverting the discretised Laplacian operator on
. The PIC method turns the Poisson part into a matrix equation by depositing the charge carried by those macro-particles on a mesh, and subsequently inverting the discretised Laplacian operator on ![]() . There are thus two components to a PIC code: 1) a Lagrangian “particle push” and 2) a Eulerian “field solve”.
. There are thus two components to a PIC code: 1) a Lagrangian “particle push” and 2) a Eulerian “field solve”.
We decided on a simple leap-frog scheme for the particle push. This 2nd order explicit symplectic integrator ensures long-time stability such Hamiltonian system. It is also excessively simple and fast to implement. We decided on a simple closest-grid-point binning of macro-particles on a regular grid to compute the charge density, and the simplest possible finite-difference scheme for solving the Poisson equation. Subject to Dirichlet boundary conditions (also chosen for simplicity), this leads to a tridiagonal linear matrix equation which is solved in ![]() time by the Thomas algorithm (Gauss-Jordan elimination). All of this is detailed in the slides attached with the python package.
time by the Thomas algorithm (Gauss-Jordan elimination). All of this is detailed in the slides attached with the python package.
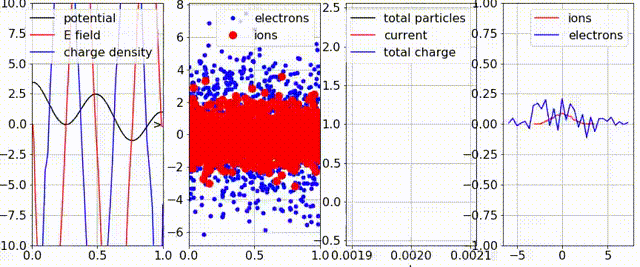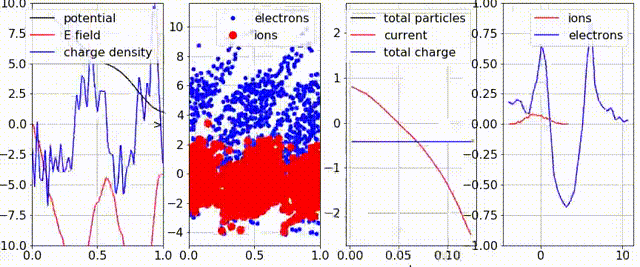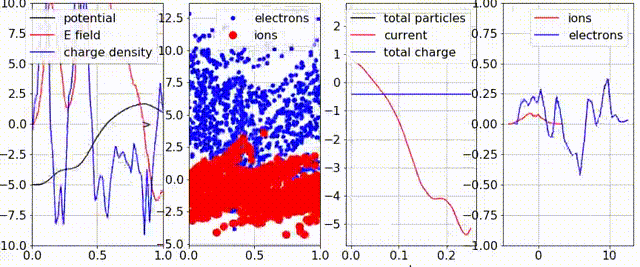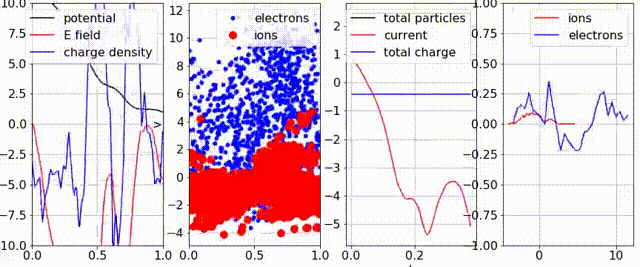
 and uniform with a “cosine” perturbation in
and uniform with a “cosine” perturbation in 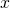 . This results in the phase-space clumps (second plot from the left).
. This results in the phase-space clumps (second plot from the left).