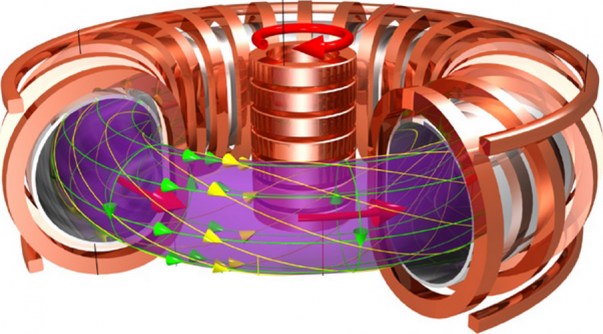
Motivation
Stellarators are weird-looking fusion devices. The reason is that ions and electrons are better confined when the magnetic field is “twisting” around the centre-line of the device called the magnetic axis.
In tokamaks, the vacuum field generated by the evenly-positioned toroidal field coils is somewhat “flat”, as shown on the figure below.

In order to generate twisting, a strong toroidal plasma current (in red in the figure below) is induced by time-varying currents in coils that are stacked through the centre of the doughnut. The toroidal plasma current produces its own poloidal component and makes the field-lines twist around the centre of the doughnut (yellow lines in the figure below). The axisymmetry and the strong twist combine to make tokamaks very efficient at confining ions and electrons (low transport).
The need for induced currents however limits the duration of tokamak discharges to finite times (as long as 15 minutes in JET); there is always a maximum current that a centre-stack coil can be ramped-up to.
Stellarators do not induce currents, so much so that the challenges of plasma control and the deleterious effect of plasma instabilities are bypassed altogether. The question is then how to produce sufficient magnetic twist from outside (external coils). There is no other way than to break the harmonious axisymmetry of tokamaks and make the coils wrap tightly around it in strange shapes.
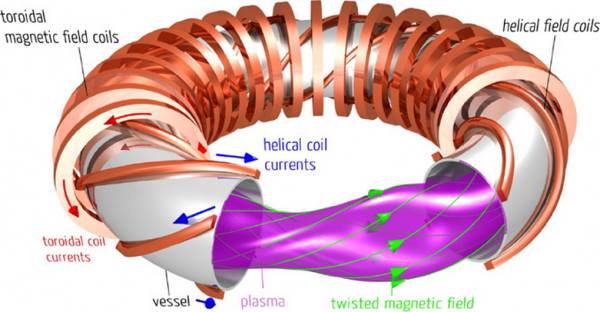
There are in fact two main ways to achieve high magnetic twist: 1) more turns in the helical coils yields a faster rotating plasma boundary , 2) non-planar shape of the centre-line yields writhing of magnetic field-lines.


The immediate questions in case 2) are what shapes produce most writhe ? What is the effect of the magnetic axis geometry on the field-line twist ? How can this effect be maximised ? We have proposed an answer by combining results from the classical theory of elasticae and a remarkable theorem in knot theory by Călugăreanu.
How to choose the magnetic axis of a stellarator ?
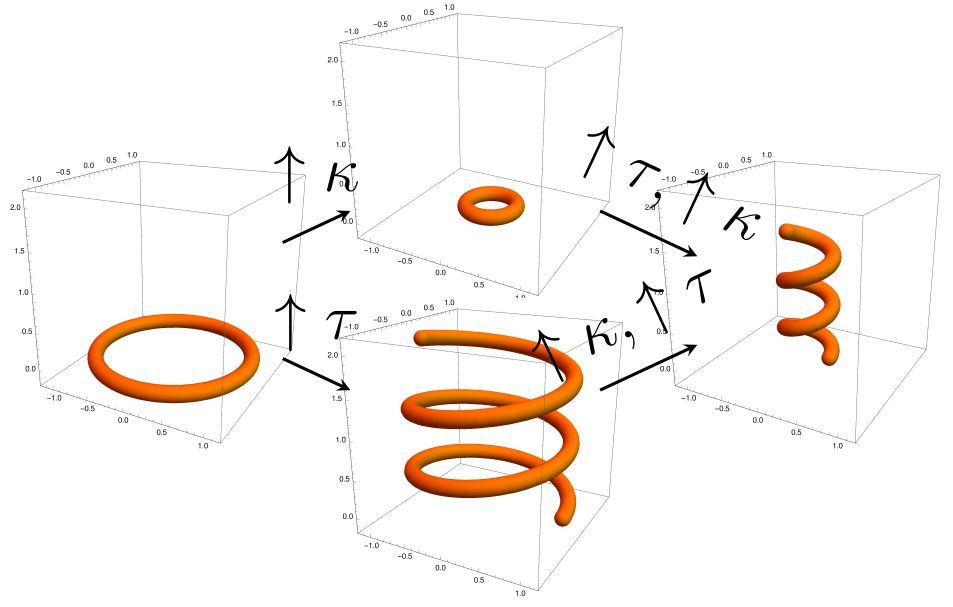
Of course, there are infinite possibilities to shape the magnetic axis of a stellarator, but a useful way to mathematically frame the problem is: find all closed curves, of fixed length, that yield a fixed amount of integrated torsion and that minimise the bending energy. This problem begs for a variational formulation based on the following cost functional
![Rendered by QuickLaTeX.com \[S[\gamma] = \lambda_1 \int\limits_\gamma ds + \lambda_2 \int\limits_\gamma \tau ds + \lambda_3 \int\limits_\gamma \frac{1}{2} \kappa^2 ds\]](https://www.pf-le.com/wp-content/ql-cache/quicklatex.com-36a82603eeed48393dff6b0be6a15ea4_l3.png)
where the first term is simply the length of the curve, the second the torsion ![]() integrated along the curve, and the third the bending energy defined as half the integral of the square of the curvature
integrated along the curve, and the third the bending energy defined as half the integral of the square of the curvature ![]() (see Frenet-Serret formulae). The parameters
(see Frenet-Serret formulae). The parameters ![]() act as Lagrange multipliers (control parameters). Solutions to this variational problem are called elasticae, and were first studied a long time ago by Euler, Bernoulli, Jacobi, etc. in the context of beam theory (building construction). Recent use of elastica theory is found for instance in the coiling of DNA.
act as Lagrange multipliers (control parameters). Solutions to this variational problem are called elasticae, and were first studied a long time ago by Euler, Bernoulli, Jacobi, etc. in the context of beam theory (building construction). Recent use of elastica theory is found for instance in the coiling of DNA.
The simplest example of an elastica (in fact the optimal solution) is a circle, where the curvature is constant and the torsion is zero. Another example, which is in fact not closed, is the helix where curvature and torsion are constant.
Related publications
| : Non-planar elasticae as optimal curves for the magnetic axis of stellarators. In: Physics of Plasmas, vol. 25, no. 9, pp. 092508, 2018. |